14 递归树

递归代码的时间复杂度分析起来很麻烦。利用递推公式求解，但是，有些情况，用递推公式的话，会涉及非常复杂的数学推导。除了用递推公式这种比较复杂的分析方法，还可以借助递归树来分析递归算法的时间复杂度。

递归树与时间复杂度分析

递归的思想就是，将大问题分解为小问题来求解，然后再将小问题分解为小小问题。这样一层一层地分解，直到问题的数据规模被分解得足够小，不用继续递归分解为止。

如果把这个一层一层的分解过程画成图，其实就是一棵树（递归树）。

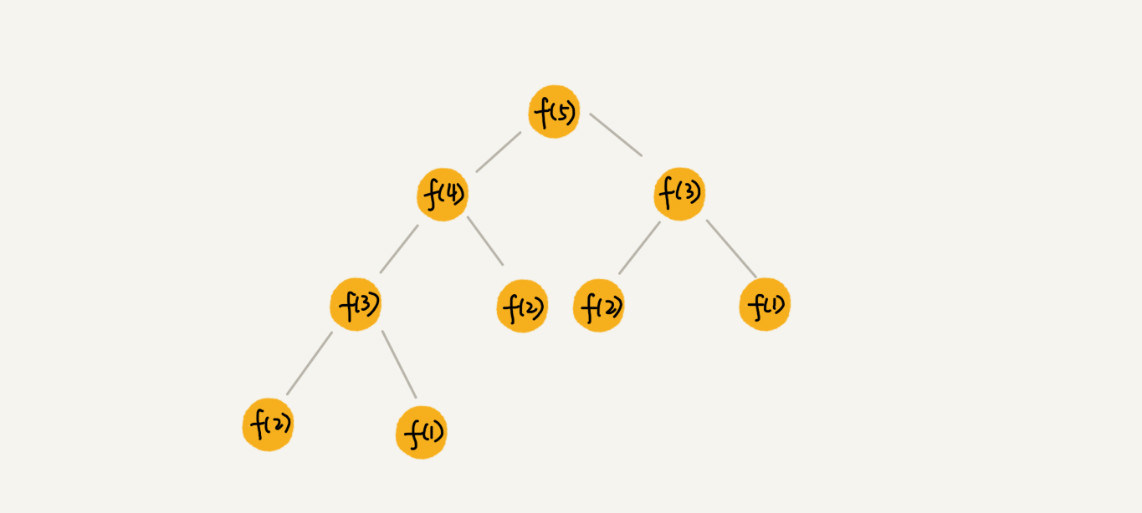
如下是一棵斐波那契数列的递归树，节点里的数字表示数据的规模，一个节点的求解可以分解为左右子节点两个问题的求解。

归并排序是一个自上而下的分治过程，每次会将数据规模一分为二。把归并排序画成递归树，如下所示：

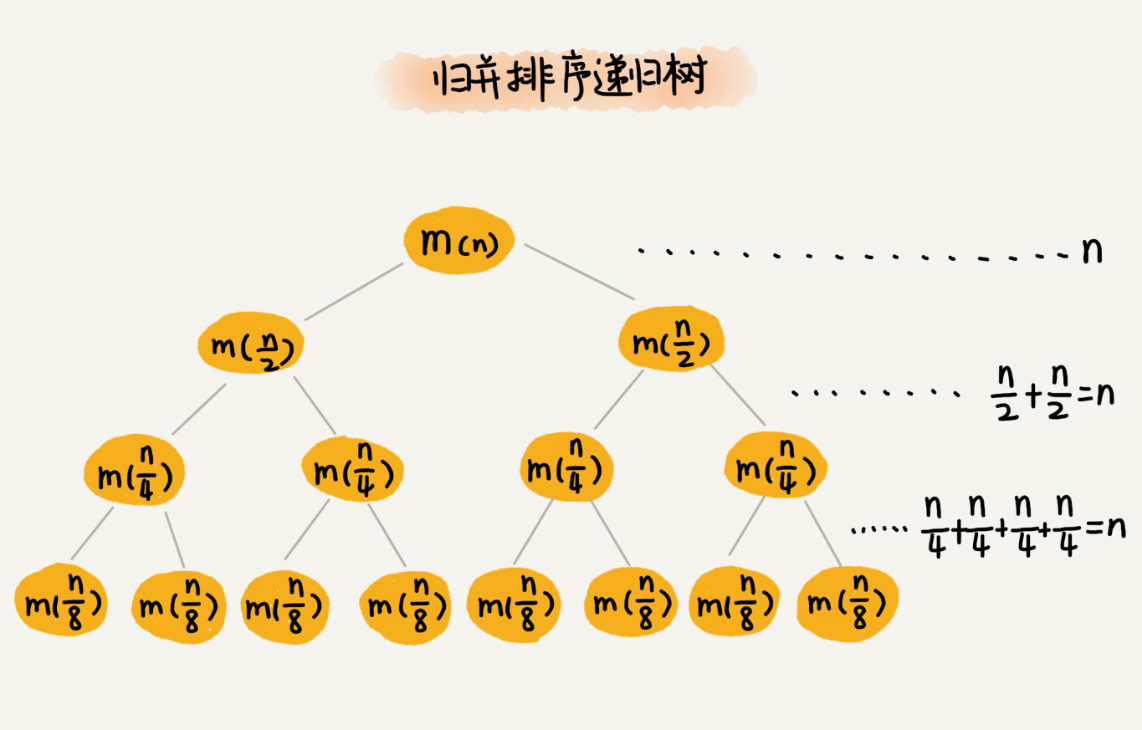
• 每次分解都是一分为二，所以代价很低，把时间上的消耗记作常量1。
• 比较耗时的是归并操作，也就是把两个子数组合并为大数组。

从图中可以看出，每一层归并操作消耗的时间总和是一样的，跟要排序的数据规模有关。把每一层归并操作消耗的时间记作n。

现在，只需要知道这棵树的高度h，用高度h乘以每一层的时间消耗n，就可以得到总的时间复杂度\(O(n∗h)\)。

从归并排序的原理和递归树，可以看出来，归并排序递归树是一棵满二叉树。满二叉树的高度大约是\(log_2n\)，所以，归并排序递归实现的时间复杂度就是\(O(nlogn)\)。