10 哈希表

散列表用的是数组支持按照下标随机访问数据的特性，时间复杂度是O(1)，所以散列表其实就是数组的一种扩展，由数组演化而来。可以说，如果没有数组，就没有散列表。

  • 通过散列函数把元素的键值映射为下标，然后将数据存储在数组中对应下标的位置。
  • 按照键值查询元素时，用同样的散列函数，将键值转化数组下标，从对应的数组下标的位置取数据。

散列表两个核心问题是散列函数设计和散列冲突解决。散列函数设计的好坏决定了散列冲突的概率，也就决定散列表的性能。

0.1. 应用

Microsoft Word中拼写检查功能的实现。

常用的英文单词有 20 万个左右，假设单词的平均长度是 10 个字母，平均一个单词占用 10 个字节的内存空间，那 20 万英文单词大约占 2MB 的存储空间，就算放大 10 倍也就是 20MB。

对于现在的计算机来说，这个大小完全可以放在内存里面，所以可以用散列表来存储整个英文单词词典。

  1. 当用户输入某个英文单词时，拿用户输入的单词去散列表中查找
  2. 如果查到，则说明拼写正确
  3. 如果没有查到，则说明拼写可能有误，给予提示

借助散列表这种数据结构，可以轻松实现快速判断是否存在拼写错误。

0.2. 散列函数

散列函数在散列表中起着非常关键的作用，它是一个函数，把它定义成 hash(key)，其中 ：

  • key 表示元素的键值
  • hash(key) 的值表示经过散列函数计算得到的散列值

散列函数设计的三点基本要求：

  1. 散列函数计算得到的散列值是一个非负整数：因为数组下标从0开始
  2. 如果 key1 = key2，那 hash(key1) == hash(key2)
  3. 如果 key1 ≠ key2，那 hash(key1) ≠ hash(key2)

对于第三点看起来合情合理，但是在真实的情况下，要想找到一个不同的 key 对应的散列值都不一样的散列函数，几乎是不可能的。

即便像业界著名的MD5、SHA、CRC等哈希算法，也无法完全避免这种散列冲突。而且，因为数组的存储空间有限，也会加大散列冲突的概率。

  • MD5（MD5 Message-Digest Algorithm）：密码散列函数，可以产生出一个128位的散列值，用于确保信息传输完整一致，曾被用于文件校验，但存在明显缺陷。
  • SHA（Secure Hash Algorithm）：密码散列函数家族，能计算出一个数字消息所对应到的，长度固定的字符串（又称消息摘要）的算法。
  • CRC（Cyclic redundancy check）：根据网络数据包或电脑文件等数据产生简短固定位数校验码的散列函数，主要用来检测或校验数据传输或者保存后可能出现的错误。

所以几乎无法找到一个完美的无冲突的散列函数，即便能找到，付出的时间成本、计算成本也是很大的，所以针对散列冲突问题，需要通过其他途径来解决。

0.3. 散列冲突

再好的散列函数也无法避免散列冲突，常用的散列冲突解决方法有两类：

  • 开放寻址法（open addressing）
  • 链表法（chaining）

0.3.1. 开放寻址法

开放寻址法的核心思想是，如果出现了散列冲突，就重新探测一个空闲位置，将其插入。

0.3.1.1. 线性探测

如何重新探测新的位置，比较简单的探测方法，线性探测（Linear Probing）。

当往散列表中插入数据时，如果某个数据经过散列函数散列之后，存储位置已经被占用了，就从当前位置开始，依次往后查找，看是否有空闲位置，直到找到为止。

在散列表中查找元素的过程有点儿类似插入过程。

  1. 通过散列函数求出要查找元素的键值对应的散列值
  2. 然后比较数组中下标为散列值的元素和要查找的元素
  3. 如果相等，则说明就是要找的元素
  4. 否则就顺序往后依次查找
  5. 如果遍历到数组中的空闲位置，还没有找到，就说明要查找的元素并没有在散列表中

散列表跟数组一样，不仅支持插入、查找操作，还支持删除操作。

对于使用线性探测法解决冲突的散列表，删除操作稍微有些特别。不能单纯地把要删除的元素设置为空。

因为在查找的时候，一旦通过线性探测方法，找到一个空闲位置，就可以认定散列表中不存在这个数据。但是，如果这个空闲位置是后来删除的，就会导致原来的查找算法失效。本来存在的数据，会被认定为不存在。

因此将删除的元素，特殊标记为 deleted。当线性探测查找的时候，遇到标记为 deleted 的空间，并不是停下来，而是继续往下探测。

线性探测法存在很大问题，当散列表中插入的数据越来越多时，散列冲突发生的可能性就会越来越大，空闲位置会越来越少，线性探测的时间就会越来越久。

极端情况下，可能需要探测整个散列表，所以最坏情况下的时间复杂度为 O(n)。同理，在删除和查找时，也有可能会线性探测整张散列表，才能找到要查找或者删除的数据。

0.3.1.2. 二次探测

为了解决开放寻址冲突的问题，所谓二次探测，跟线性探测很像：

  • 线性探测：每次探测的步长是 1，探测的下标序列就是 hash(key)+0，hash(key)+1，hash(key)+2……
  • 二次探测：探测的步长就变成了原来的“二次方”，探测的下标序列就是 hash(key)+0，hash(key)+1^2，hash(key)+2^2……

0.3.1.3. 双重散列

为了解决开放寻址冲突的问题，所谓双重散列，就是不仅要使用一个散列函数。

使用一组散列函数 hash1(key)，hash2(key)，hash3(key)……

先用第一个散列函数，如果计算得到的存储位置已经被占用，再用第二个散列函数，依次类推，直到找到空闲的存储位置。

不管采用哪种探测方法，当散列表中空闲位置不多的时候，散列冲突的概率就会大大提高。为了尽可能保证散列表的操作效率，一般情况下，会尽可能保证散列表中有一定比例的空闲槽位，用装载因子（load factor）来表示空位的多少。

装载因子的计算公式是：散列表的装载因子=填入表中的元素个数/散列表的长度，装载因子越大，说明空闲位置越少，冲突越多，散列表的性能会下降。

0.3.2. 链表法

链表法是一种更常用的散列冲突解决办法，相比开放寻址法，它要简单很多。

如下图所示，在散列表中，每个“桶（bucket）”或者“槽（slot）”会对应一条链表，所有散列值相同的元素都放到相同槽位对应的链表中。

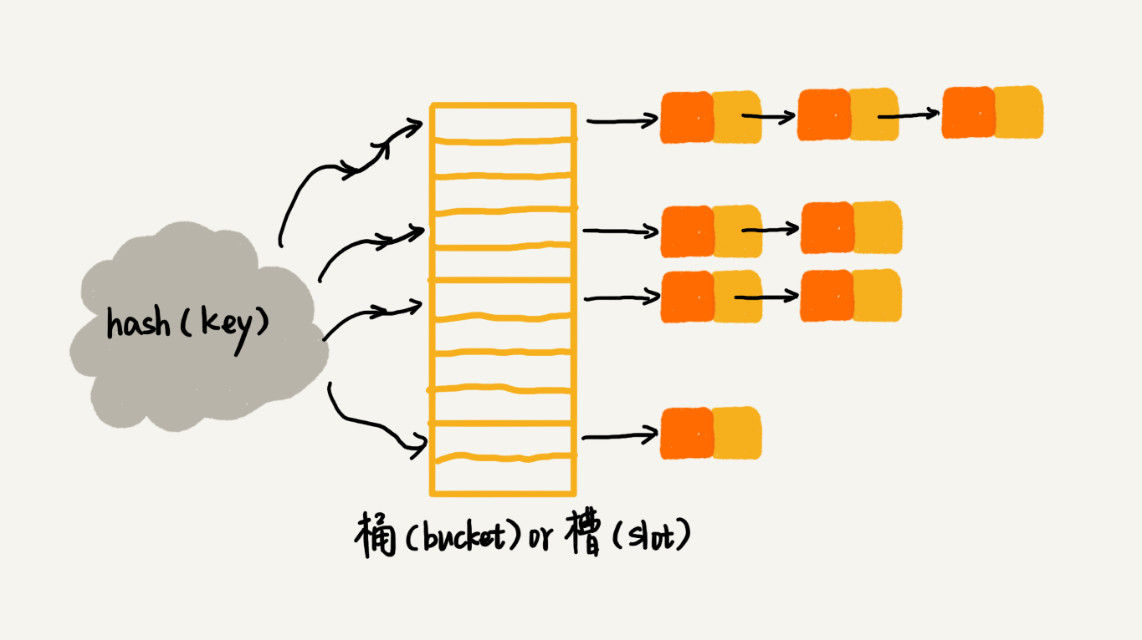
image

  • 插入时，只需要通过散列函数计算出对应的散列槽位，将其插入到对应链表中即可，所以插入的时间复杂度是 O(1)。
  • 查找/删除时，通过散列函数计算出对应的槽，然后遍历链表查找或者删除。

查找或删除这两个操作的时间复杂度跟链表的长度 k 成正比即O(k)。对于散列比较均匀的散列函数来说，理论上讲，\(k=\frac{n}{m}\)，其中 n 表示散列中数据的个数，m 表示散列表中“槽”的个数。

0.4. 设计散列表

散列表的查询效率并不能笼统地说成是 O(1)，这与散列函数、装载因子、散列冲突等都有关系。如果散列函数设计得不好，或者装载因子过高，都可能导致散列冲突发生的概率升高，查询效率下降。

在极端情况下，恶意攻击者通过精心构造的数据，使得所有的数据都散列到同一个槽里。如果使用的是基于链表的冲突解决方法，那散列表就会退化为链表，查询的时间复杂度就从 O(1) 急剧退化为 O(n)。

  • 如果散列表中有 10 万个数据，退化后的散列表查询的效率就下降了 10 万倍。
  • 如果之前运行 100 次查询只需要 0.1 秒，那现在就需要 10000 秒。

这样有可能因为查询操作消耗大量 CPU 或者线程资源，导致系统无法响应其他请求，从而达到拒绝服务攻击（DoS）的目的。这就是散列表碰撞攻击的基本原理。

需要设计一个可以应对各种异常情况的工业级散列表，来避免在散列冲突的情况下，散列表性能的急剧下降，并且能抵抗散列碰撞攻击。

散列函数设计的好坏，决定了散列表冲突的概率大小，也直接决定了散列表的性能：

  1. 散列函数的设计不能太复杂：散列函数太复杂，会消耗很多计算时间，间接的影响到散列表的性能
  2. 散列函数生成的值要尽可能随机并且均匀分布：这样才能避免或者最小化散列冲突，即便出现冲突，散列到每个槽里的数据也会比较平均，不会出现某个槽内数据特别多的情况

实际工作中，还需要综合考虑各种因素：关键字的长度、特点、分布、还有散列表的大小等。

0.4.1. 常用散列函数设计方法

  1. 数据分析法：例如，分析参赛编号的特征，把编号中的后两位作为散列值；手机号码前几位重复的可能性很大，但是后面几位就比较随机，可以取手机号的后四位作为散列值。
  2. 设计函数：例如，Microsoft Word中拼写检查功能中，将单词中每个字母的ASCll 码值“进位”相加，然后再跟散列表的大小求余、取模，作为散列值。比如，英文单词 nice：hash("nice")=\(\frac{(('n'-'a')*26*26*26+('i'-'a')*26*26+('c'-'a')*26+('e'-'a'))}{78978}\)
  3. 直接寻址法
  4. 平方取中法
  5. 折叠法
  6. 随机数法

0.4.2. 避免装载因子过大

装载因子越大，说明散列表中的元素越多，空闲位置越少，散列冲突的概率就越大：

  • 插入的过程要多次寻址或者遍历很长的链表
  • 查找的过程同样很慢

对于没有频繁插入和删除的静态数据集合，根据数据的特点、分布等，设计出完美的、极少冲突的散列函数。

对于动态散列表，数据集合频繁变动，事先无法预估将要加入的数据个数，所以无法事先申请一个足够大的散列表。随着数据慢慢加入，装载因子就会慢慢变大。当装载因子大到一定程度之后，散列冲突就会变得不可接受。

当装载因子过大时，进行动态扩容重新申请一个更大的散列表，将数据搬移到新散列表中。

假设每次扩容都申请一个原来散列表大小两倍的空间。如果原来散列表的装载因子是 0.8，那经过扩容之后，新散列表的装载因子就下降为原来的一半，变成了 0.4。

  • 针对数组的扩容，数据搬移操作比较简单。
  • 针对散列表的扩容，数据搬移操作要复杂很多。因为散列表的大小变了，数据的存储位置也变了，需要通过散列函数重新计算每个数据的存储位置。

散列表中插入一个数据：

  • 最好情况下，不需要扩容，最好时间复杂度是 O(1)。
  • 最坏情况下，散列表装载因子过高，启动扩容重新申请内存空间，重新计算哈希位置，并且搬移数据，时间复杂度是 O(n)。

用摊还分析法，均摊情况下，时间复杂度接近最好情况，就是 O(1)。

实际上，对于动态散列表，随着数据的删除，散列表中的数据会越来越少，空闲空间会越来越多：

  • 如果对空间消耗敏感，可以在装载因子小于某个值之后，启动动态缩容
  • 如果对执行效率敏感，能够容忍多消耗一点内存空间，就不用费劲缩容

当散列表的装载因子超过某个阈值时，就需要进行扩容，装载因子阈值需要选择得当：

  • 如果太大，会导致冲突过多
  • 如果太小，会导致内存浪费严重

装载因子阈值的设置要权衡时间、空间复杂度：

  • 如果内存空间不紧张，对执行效率要求很高，可以降低负载因子的阈值
  • 如果内存空间紧张，对执行效率要求又不高，可以增加负载因子的值，甚至可以大于 1

0.4.3. 避免低效扩容

0.4.3.1. 对于插入操作

大部分情况下，动态散列表插入数据的效率很高，只有在装载因子到达阈值需要先扩容在插入，这时插入数据很慢甚至无法接受。散列表中已有的数据越多，扩容越慢，需要重新计算每一个值的位置。

为了解决一次性扩容耗时过多的情况，可以将扩容操作穿插在插入操作的过程中，分批完成。当装载因子触达阈值之后，只申请新空间，但并不将老的数据搬移到新散列表中。

  1. 当新数据要插入时，将新数据插入新散列表中，并从旧散列表中拿出一个数据放入到新散列表
  2. 每插入一个数据都重复上述过程
  3. 多次插入后，旧散列表中数据就全部搬移到新散列表中了

这样没有集中的一次性数据搬移，插入操作就都变得很快了。

0.4.3.2. 对于查询操作

为了兼容了新、旧散列表中的数据：

  1. 先从新散列表中查找
  2. 如果没有找到，再去旧散列表中查找

通过这样均摊的方法，将一次性扩容的代价，均摊到多次插入操作中，就避免了一次性扩容耗时过多的情况。这种实现方式，任何情况下，插入一个数据的时间复杂度都是 O(1)。

0.4.4. 散列冲突解决办法

在实际的软件开发中，开放寻址法和链表法是非常常用的两种解决散列冲突的方法，如：

  • Java 中 LinkedHashMap 采用链表法解决冲突
  • Java 中 ThreadLocalMap 采用线性探测的开放寻址法解决冲突

下面对这两种冲突解决版本优劣和适用场景进行比较。

0.4.4.1. 开放寻址法

  • 优点：数据都存储在数组中，有效地利用 CPU 缓存加快查询速度。这种方法实现的散列表，序列化起来比较简单（链表法包含指针，序列化起来就没那么容易），序列化在很多场合都会用到。

  • 缺点：删除数据的时候比较麻烦，需要特殊标记已经删除掉的数据。所有的数据都存储在一个数组中，冲突的代价更高。所以，使用开放寻址法解决冲突的散列表，装载因子的上限不能太大。这也导致这种方法比链表法更浪费内存空间。

当数据量比较小、装载因子小的时候，适合采用开放寻址法。这也是 Java 中的 ThreadLocalMap 使用开放寻址法解决散列冲突的原因。

0.4.4.2. 链表法

  • 优点：

    • 对内存的利用率比开放寻址法要高，因为链表结点在需要时才创建，不需要事先申请好。
    • 对大装载因子的容忍度更高，开放寻址法只能适用装载因子小于 1 的情况，对于链表法，只要散列函数的值随机均匀，即便装载因子变成 10，也就是链表的长度变长了而已，虽然查找效率有所下降，但是比起顺序查找还是快很多。

  • 缺点：

    • 链表要存储指针，所以对于比较小的对象的存储，是比较消耗内存的，可能会让内存的消耗翻倍。（如果存储的对象的大小远远大于一个指针的大小（4或8字节），那链表中指针的内存消耗可以忽略）。
    • 链表中结点是零散分布在内存中的，对 CPU 缓存不友好，这对于执行效率也有一定的影响。

实际上，对链表法稍加改造，可以实现更加高效的散列表，将链表改造为其他高效的动态数据结构，比如跳表、红黑树。这样，即便出现散列冲突，极端情况下，所有的数据都散列到同一个桶内，那最终退化成的散列表的查找时间也只不过是 O(logn)，这样有效避免了散列碰撞攻击。

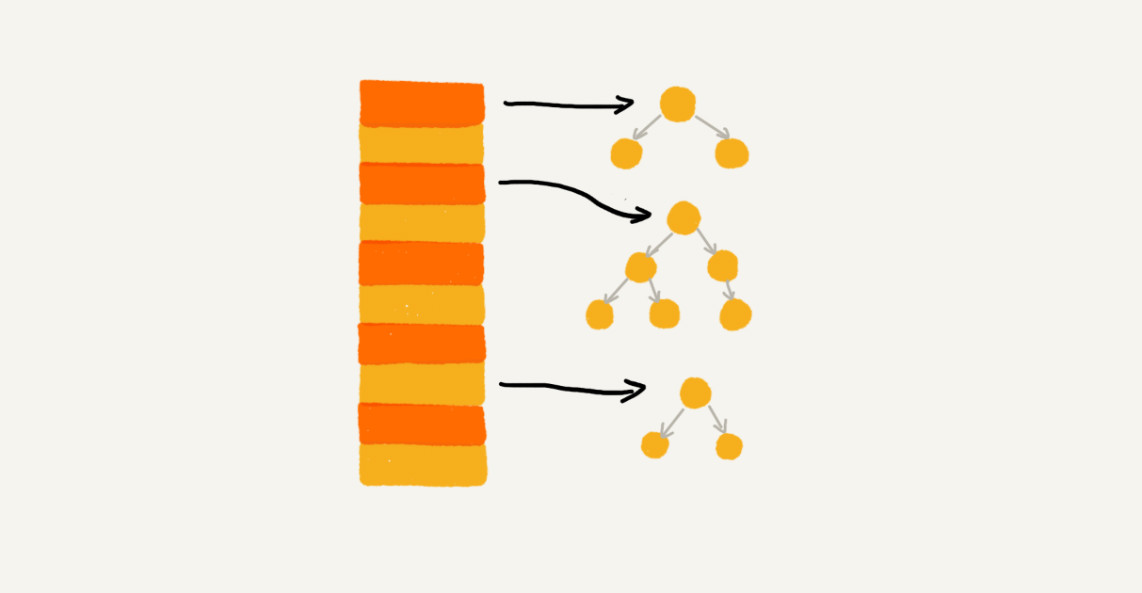
image

基于链表的散列冲突处理方法比较适合存储大对象、大数据量的散列表，而且，它更加灵活，支持更多的优化策略，比如用红黑树代替链表。

0.5. 工业级散列表

Java中的HashMap。

  1. 初始化大小：默认的初始大小是 16，这个默认值可以设置，如果事先知道大概的数据量，可以通过修改默认初始大小，减少动态扩容的次数，这样会大大提高 HashMap 的性能。
  2. 装填因子和动态扩容：最大装载因子默认是 0.75，当元素个数超过 0.75*capacity（capacity表示散列表的容量）时，会启动扩容，每次扩容都会扩容为原来的两倍大小。
  3. 散列冲突解决方法：底层采用链表法来解决冲突，即使负载因子和散列函数设计得再合理，也免不了会出现拉链过长的情况，一旦出现拉链过长，则会严重影响 HashMap 的性能。在 JDK1.8 中，对 HashMap 做进一步优化，引入了红黑树。当链表长度太长（默认超过 8）时，链表就转换为红黑树。当红黑树结点个数少于 8 个时，又会将红黑树转化为链表。

  4. 散列函数：

    int hash(Object key) {
    int h = key.hashCode()；    // 返回 Java 对象的 hash code
    return (h ^ (h >>> 16)) & (capicity -1); // capicity表示散列表的大小
}

public int hashCode() {
int var1 = this.hash;
if(var1 == 0 && this.value.length > 0) {
    char[] var2 = this.value;
    for(int var3 = 0; var3 < this.value.length; ++var3) {
    var1 = 31 * var1 + var2[var3];
    }
    this.hash = var1;
}
return var1;
}

利用红黑树快速增删改查的特点，提高 HashMap 的性能。在数据量较小的情况下，红黑树要维护平衡，比起链表来，性能上的优势并不明显。

工业级的散列表应该具有的特性：

  1. 支持快速的查询、插入、删除操作
  2. 内存占用合理，不能浪费过多的内存空间
  3. 性能稳定，极端情况下，散列表的性能也不会退化到无法接受的情况

实现这样的散列表从这三个方面来考虑：

  1. 设计一个合适的散列函数
  2. 定义装载因子阈值，并且设计动态扩容策略
  3. 选择合适的散列冲突解决方法

还要结合具体的业务场景、具体的业务员数据来具体分析。

0.5.1. LRU缓存淘汰算法

借助散列表，可以把 LRU 缓存淘汰算法的时间复杂度降低为 O(1)。

通过链表实现 LRU 缓存淘汰算法的，需要维护一个按照访问时间从大到小有序排列的链表结构。

  1. 当缓存空间不够，需要淘汰一个数据，就直接将链表头部的结点删除。
  2. 当要缓存某个数据时，先在链表中查找这个数据。如果没有找到，则直接将数据放到链表的尾部；如果找到了，就把它移动到链表的尾部。查找数据需要遍历链表，所以单纯用链表实现的 LRU 缓存淘汰算法的时间复杂是 O(n)。

一个缓存（cache）系统主要包含下面这三个操作：

  1. 往缓存中查找一个数据；
  2. 从缓存中删除一个数据；
  3. 在缓存中添加一个数据。

这三个操作都要涉及“查找”操作，如果单纯采用链表，时间复杂度只能是 O(n)。

如果将散列表和链表组合使用，可以将这三个操作的时间复杂度都降低到 O(1)，如下图所示：

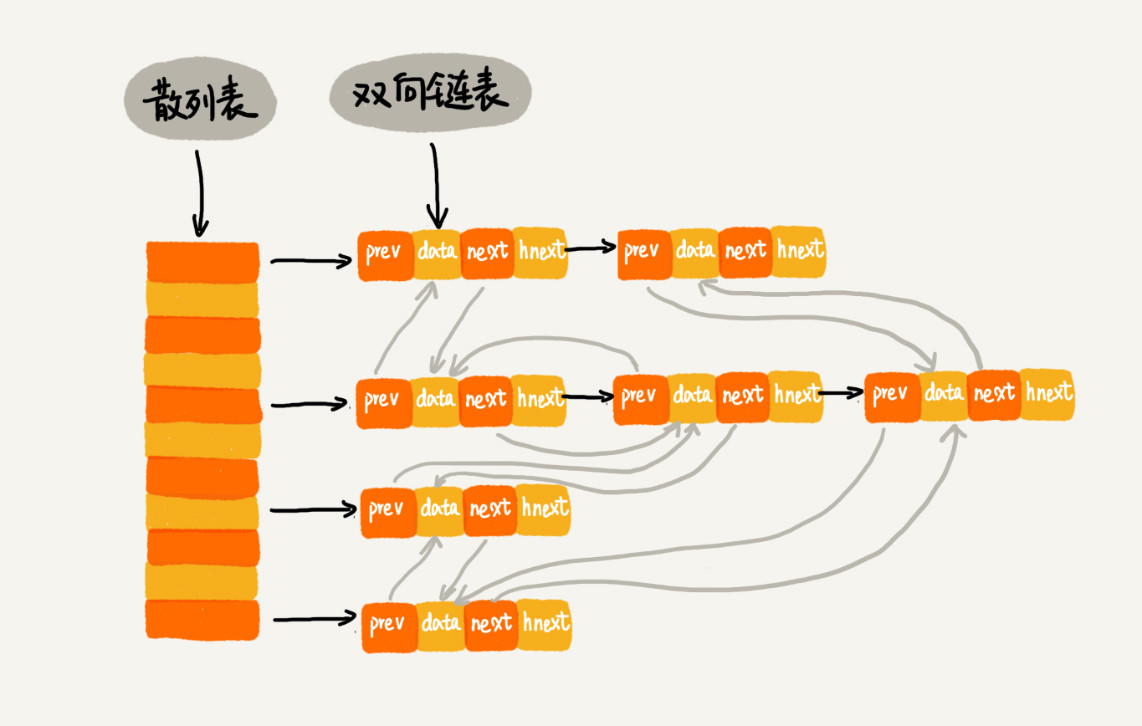
image

使用双向链表存储数据，链表中的每个结点包括：

  1. 存储数据data
  2. 前驱指针prev
  3. 后继指针next
  4. 特殊字段hnext

LRU中的散列表是通过链表法解决散列冲突的，所以每个结点会在两条链中：

  • 一个链是双向链表：前驱和后继指针是为了将结点串在双向链表中
  • 一个链是散列表中的拉链：hnext指针是为了将结点串在散列表的拉链中

使用散列表和双向链表的组合存储结果，实现一个换成系统三个操作的时间复杂度是O(1):

  1. 查找数据：散列表中查找数据的时间复杂度接近O(1)，找到数据后将它移动到双向链表的尾部（LRU是从头开始删除的）
  2. 删除数据：借助散列表查找待删除数据时间复杂度O(1)，借助双向链表删除数据时间复杂度O(1)
  3. 添加数据：
    1. 先查找，存在则移至尾部
    2. 不存在则判断链表是否已满，
      1. 满则删除双链表头部，然后添加到尾部
      2. 不满则直接添加到尾部

整个过程中，查找操作都借助散列表在O(1)完成，添加和删除操作都借助双向链表在O(1)完成。所以通过散列表和双向链表的组合使用，实现了一个高效的、支持 LRU 缓存淘汰算法的缓存系统原型。

0.5.2. Redis有序集合

在有序集合中，每个成员对象有两个重要的属性，key（键值）和 score（分值）。不仅会通过 score 来查找数据，还通过 key 来查找数据。

所以Redis有序集合的操作包括：

  1. 添加一个成员对象；
  2. 按照键值来删除一个成员对象；
  3. 按照键值来查找一个成员对象；
  4. 按照分值区间查找数据；
  5. 按照分值从小到大排序成员变量；

如果仅按照分值将成员对象组织成跳表的结构，那按照键值来删除、查询成员对象就会很慢。

解决方法与 LRU 缓存淘汰算法的解决方法类似。

按照分值构建跳表后再按照键值构建散列表，这样按照 key 来删除、查找一个成员对象的时间复杂度就变成了 O(1)。同时，借助跳表结构，其他操作也非常高效。

实际上，Redis 有序集合的操作还有查找成员对象的排名（Rank）或者根据排名区间查找成员对象。这个功能单纯用这种组合结构就无法高效实现了。

0.5.3. Java LInkedHashMap

  • HashMap 底层是通过散列表实现的
  • LinkedHashMap 底层是通过散列表和双向链表组合在一起实现的（Linked指双向链表而不是用链表解决散列冲突）

在新建LinkedHashMap是可以传参设定是否按照访问时间排序，即是否启用LRU缓存淘汰策略。

散列表和链表经常一起使用的原因：

  • 散列表虽然支持非常高效的数据插入、删除、查找操作，但数据都是通过散列函数打乱之后无规律存储的，无法支持按照某种顺序快速地遍历数据。如果希望按照顺序遍历散列表中的数据，就需要将数据拷贝到数组中，然后排序，再遍历。
  • 散列表是动态数据结构，不停地有数据的插入、删除，所以每当希望按顺序遍历散列表中数据时，都需要先排序，那效率势必会很低。为了解决这个问题，将散列表和链表（或者跳表）结合在一起使用。
上次修改: 28 June 2020