Promacanthus

0.1. 定义
0.2. 时间复杂度
0.3. 最简单情况的代码实现
0.4. 应用场景的局限性
0.5. 常见变形问题的代码实现

0.1. 定义

针对有序数据集合的查找算法：二分查找（Binary Search）算法，也叫折半查找算法。

假设有10个数据：8，11，19，23，27，33，45，55，67，98，快速找到19这个值是否在数据中。

利用二分思想，每次都与区间的中间数据比对大小，缩小查找区间的范围。过程如下图所示，其中，low 和 high 表示待查找区间的下标，mid 表示待查找区间的中间元素下标。

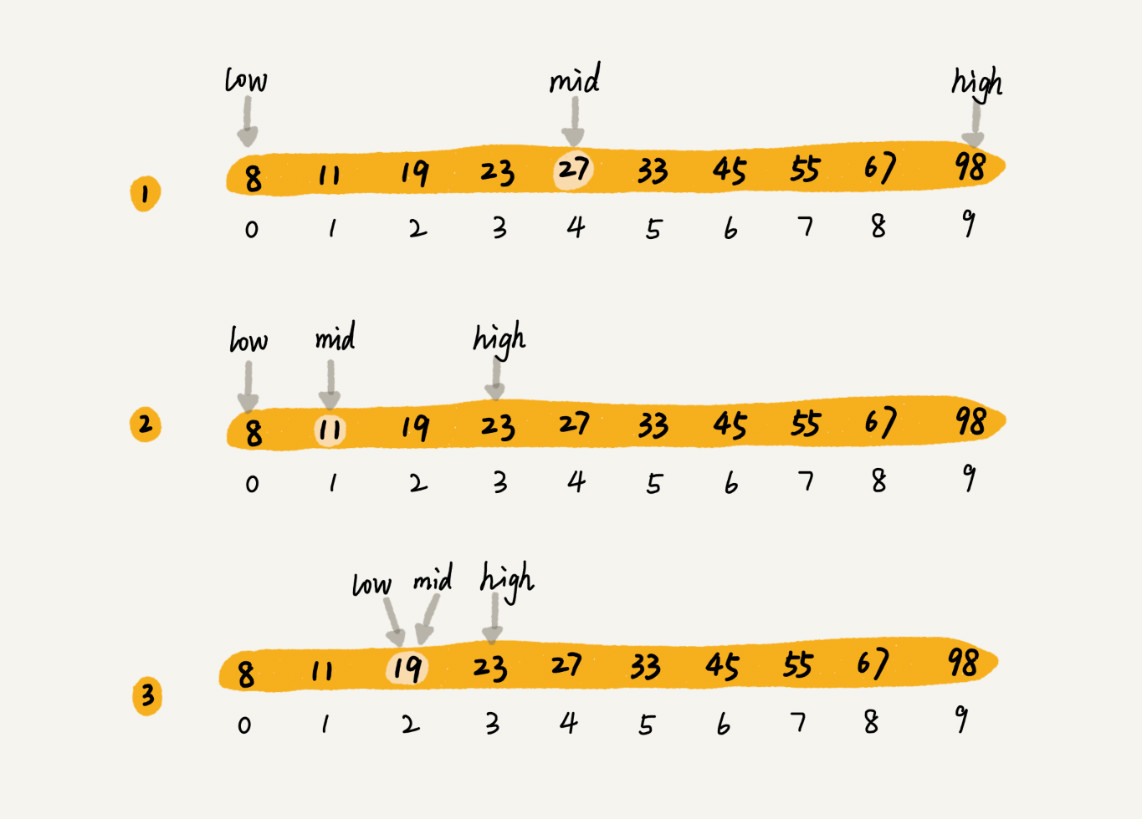
二分查找针对的是一个有序的数据集合，查找思想有点类似分治思想。
每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为 0。

0.2. 时间复杂度

假设数据大小是 n，每次查找后数据都会缩小为原来的一半，也就是会除以 2。最坏情况下，直到查找区间被缩小为空，才停止。

这是一个等比数列。
其中 \(\frac{n}{2^k}=1\) 时，k 的值就是总共缩小的次数。
每一次缩小操作只涉及两个数据的大小比较，所以，经过了 k 次区间缩小操作，时间复杂度是 \(O(k)\)。
通过 \(\frac{n}{2^k}=1\)，求得 \(k=log2n\)，时间复杂度是 \(O(logn)\)。

\(O(logn)\) 这种对数时间复杂度，是一种极其高效的时间复杂度，有时甚至比时间复杂度是常量级 \(O(1)\) 的算法还要高效。

0.3. 最简单情况的代码实现

最简单的情况就是有序数组中不存在重复元素。

创建三个变量low、high、mid 都是数组下标，
其中 low 和 high 表示当前查找的区间范围，初始 low=0， high=n-1。
mid 表示\([low, high]\)的中间位置。
通过对比 \(a[mid]\)与 value 的大小，来更新接下来要查找的区间范围，直到找到或者区间缩小为 0，就退出。

注意：

循环退出条件：是 low>=high，而不是 low>igh
mid的取值：\(mid=\frac{low+high}{2}\)在数据较大时可能溢出，改成\(low+\frac{(high-low)}{2}\)，优化性能可以将除法运算改为位运算low+((high-low)>>1)
low和high的更新：low=mid+1，high=mid-1，如果直接写成 low=mid 或者 high=mid，就可能会发生死循环

也可以使用递归实现：

递推公式：binarySearch(p...r,value)=binarySearch(p...mid-1,value) or binarySearch(mid+1...r,value)
终止条件：A[mid]=value or low >= high

0.4. 应用场景的局限性

二分查找依赖的是顺序表结构（简单点说就是数组）：因为二分查找算法需要按照下标随机访问元素
二分查找针对的是有序数据：如果数据没有序，需要先排序，排序的时间复杂度最低是 \(O(nlogn)\)。所以，如果针对一组静态数据（没有频繁地插入、删除），可以进行一次排序，多次二分查找。这样排序的成本可被均摊，二分查找的边际成本就会比较低
数据量太小不适合二分查找：数据量太小，遍历数组就足够（如果数据之间的比较操作非常耗时，需要尽可能减少比较次数，推荐使用二分查找）
数据量太大也不适合二分查找：底层依赖数组，数组实现随机访问需要内存中连续的空间，这个条件比较苛刻，所以太大的数据用数组存储就比较吃力，就不能用二分查找

0.5. 常见变形问题的代码实现

有序数据集合中不存在重复的数据。

0.5.1. 查找第一个值等于给定值的元素

a[mid]跟要查找的 value 的大小关系有三种情况：

对于 a[mid]>value 的情况，更新 high=mid-1
对于 a[mid]<value 的情况，更新 low=mid+1
对于 a[mid]=value 的情况
- 如果查找的是任意一个值等于给定值的元素，当 a[mid] 等于要查找的值时，a[mid]就是要找的元素。
- 如果查找的是第一个值等于给定值的元素，当 a[mid] 等于要查找的值时，就需要确认一下这个 a[mid]是不是第一个值等于给定值的元素。

func BinarySearchFirst(list []int, value int) int {
 low := 0
 high := len(list) - 1

 for low <= high {
  mid := low + ((high - low) >> 1)
  if list[mid] < value {
   low = mid + 1
  } else if list[mid] > value {
   high = mid - 1
  } else {
   if mid == 0 || list[mid-1] != value {
    return mid
   } else {
    high = mid - 1
   }
  }
 }

 return -1
}

看第 12 行代码。

如果 mid 等于 0，那这个元素已经是数组的第一个元素；
如果 mid 不等于 0，但 a[mid] 的前一个元素 a[mid-1] 不等于 value，那也说明 a[mid]就是要找的第一个值等于给定值的元素。
如果经过检查之后发现 a[mid]前面的一个元素 a[mid-1]也等于 value，那说明此时的 a[mid]肯定不是要查找的第一个值等于给定值的元素。更新 high=mid-1，要找的元素肯定出现在[low, mid-1]之间。

0.5.2. 查找最后一个值等于给定值的元素

基于上面的分析：

将第12行代码中if的判定条件修改为mid == len(a)-1 || list[mid+1] != value
将第15行代码修改为low=mid+1

0.5.3. 查找第一个大于等于给定值的元素

func BinarySearchGE(list []int, value int) int {
 length := len(list)
 low := 0
 high := length - 1

 for low <= high {
  mid := low + ((high - low) >> 1)
  if list[mid] >= value {
   if mid == 0 || list[mid-1] < value {
    return mid
   } else {
    high = mid - 1
   }
  } else {
   low = mid + 1
  }
 }
 return -1
}

看第7、8行代码：

如果list[mid]>=value，且mid==0，那就是要查找的值
如果list[mid]的前一个值小于value，那就是要查找的值
否则说明要查找的值在[low,mid-1]之间
如果list[mid]<value，说明要查找的之在[mid+1,high]之间

0.5.4. 查找最后一个小于等于给定值的元素

func BinarySearchLE(list []int, value int) int {
 length := len(list)
 low := 0
 high := length - 1

 for low <= high {
  mid := low + ((high - low) >> 1)
  if list[mid] > value {
   high = mid - 1
  } else {
   if mid == len(list)-1 || list[mid+1] > value {
    return mid
   } else {
    low = mid + 1
   }
  }
 }
 return -1
}

实际上，求“值等于给定值”的二分查找确实不怎么会被用到，二分查找更适合用在“近似”查找问题，在这类问题上，二分查找的优势更加明显。

上述这些变体的二分查找算法很容易因为细节处理不好而产生 Bug，这些容易出错的细节有：

终止条件
区间上下界更新方法
返回值选择

08 二分查找