06 递归
0.1. 递归定义
递归是一种应用非常广泛的算法(或者编程技巧)。很多数据结构和算法的编码实现都要用到递归,比如:
- DFS深度优先搜索
- 前中后序二叉树遍历
标准的递归求解问题的分解过程:
- 去的过程叫“递”,
- 回来的过程叫“归”。
基本上,所有的递归问题都可以用递推公式来表示,如f(n)=f(n-1)+1,其中f(1)=1转换为代码:
func f(n int) int { if n == 1 { return 1 } return f(n-1) + 1 }
0.1.1. 递归需要满足的三个条件
只要同时满足以下三个条件,就可以用递归来解决。
- 一个问题的解可以分解为几个子问题(数据规模更小的问题)的解
- 这个问题与分解之后的子问题,除了数据规模不同,求解思路完全一样
- 存在递归终止条件:把问题分解为子问题,把子问题再分解为子子问题,一层一层分解下去,不能存在无限循环
0.2. 编写递归代码
写递归代码最关键的是写出递推公式,找到终止条件,剩下将递推公式转化为代码就很简单了。
假如这里有 n 个台阶,每次你可以跨 1 个台阶或者 2 个台阶,请问走这 n 个台阶有多少种走法?如果有 7 个台阶,你可以 2,2,2,1 这样子上去,也可以 1,2,1,1,2 这样子上去,总之走法有很多,那如何用编程求得总共有多少种走法呢?
实际上,可以根据第一步的走法把所有走法分为两类:
- 第一类是第一步走了 1 个台阶
- 另一类是第一步走了 2 个台阶
所以 n 个台阶的走法就等于先走 1 阶后,n-1 个台阶的走法,加上先走 2 阶后,n-2 个台阶的走法。用公式表示就是:f(n) = f(n-1)+f(n-2)。
有了递推公式,递归代码基本上就完成了一半。
再来看下终止条件,当有一个台阶时,不需要再继续递归,就只有一种走法,所以 f(1)=1。
可以用 n=2,n=3 这样比较小的数试验一下,上述递归终止条件是否满足。
n=2时,f(2)=f(1)+f(0)。如果递归终止条件只有一个f(1)=1,那f(2)就无法求解了- 所以,还要有
f(0)=1,表示走 0 个台阶有一种走法,不过这样子看起来就不符合正常的逻辑思维了 - 所以,可以把
f(2)=2,作为一种终止条件,表示走 2 个台阶,有两种走法,一步走完或者分两步来走 n=3时,f(3)=f(2)+f(1),求解为3,终止条件正确。
综上,递推公式和终止条件并转化为代码:
/* 递推公式:f(n)=f(n-1)+f(n-2) 终止条件:f(1)=1,f(2)=2 */ func f(n int) int { if n == 1 { return 1 } if n == 2 { return 2 } return f(n-1) + f(n-2) }
写递归代码的关键就是找到如何将大问题分解为小问题的规律,并且基于此写出递推公式,然后再推敲终止条件,最后将递推公式和终止条件翻译成代码。
当递归调用只有一个分支,即“一个问题只需要分解为一个子问题”时,很容易能够想清楚“递“和”归”的每一个步骤,所以写起来、理解起来都不难。但是,当一个问题要分解为多个子问题的情况,递归代码就没那么好理解了,人脑几乎没办法把整个“递”和“归”的过程一步一步都想清楚。
计算机擅长做重复的事情,所以递归正和它的胃口,而人脑更喜欢平铺直叙的思维方式。当我们看到递归时,总想把递归平铺展开,脑子里就会循环,一层一层往下调,然后再一层一层返回,试图想搞清楚计算机每一步都是怎么执行的,这样就很容易被绕进去。对于递归代码,这种试图想清楚整个递和归过程的做法,实际上是进入了一个思维误区。很多时候,理解起来比较吃力,主要原因就是自己给自己制造了这种理解障碍。
正确的思维方式应该是:如果一个问题
A可以分解为若干子问题B、C、D,可以假设子问题B、C、D已经解决,在此基础上思考如何解决问题A。而且,只需要思考问题A与子问题B、C、D两层之间的关系即可,不需要一层一层往下思考子问题与子子问题,子子问题与子子子问题之间的关系。屏蔽掉递归细节,这样子理解起来就简单多了。
因此,编写递归代码的关键是,只要遇到递归,就把它抽象成一个递推公式,不用想一层层的调用关系,不要试图用人脑去分解递归的每个步骤。
- 写出递推公式
- 找到终止条件
- 翻译成递归代码
0.3. 递归遇到的问题
0.3.1. 警惕堆栈溢出
在实际的软件开发中,编写递归代码时,会遇到很多问题,比如堆栈溢出。而堆栈溢出会造成系统性崩溃,后果会非常严重。
回顾上一节内容“栈”,函数调用会使用栈来保存临时变量。每调用一个函数,都会将临时变量封装为栈帧压入内存栈,等函数执行完成返回时,才出栈。系统栈或者虚拟机栈空间一般都不大。如果递归求解的数据规模很大,调用层次很深,一直压入栈,就会有堆栈溢出的风险。
以Java为例,将JVM的堆栈大小设置为1KB,在求解较大数据规模时会出现如下堆栈报错Exception in thread "main" java.lang.StackOverflowError。
可以通过在代码中限制递归调用的最大深度的方式来解决这个问题。递归调用超过一定深度(比如 1000)之后,就不继续往下再递归了,直接返回报错。
但这种做法并不能完全解决问题,因为最大允许的递归深度跟当前线程剩余的栈空间大小有关,事先无法计算。如果实时计算,代码过于复杂,就会影响代码的可读性。所以,如果最大深度比较小,比如 10、50,就可以用这种方法,否则这种方法并不是很实用。
0.3.2. 警惕重复计算
使用递归时还会出现重复计算的问题,例如上面求解楼梯走法的问题:
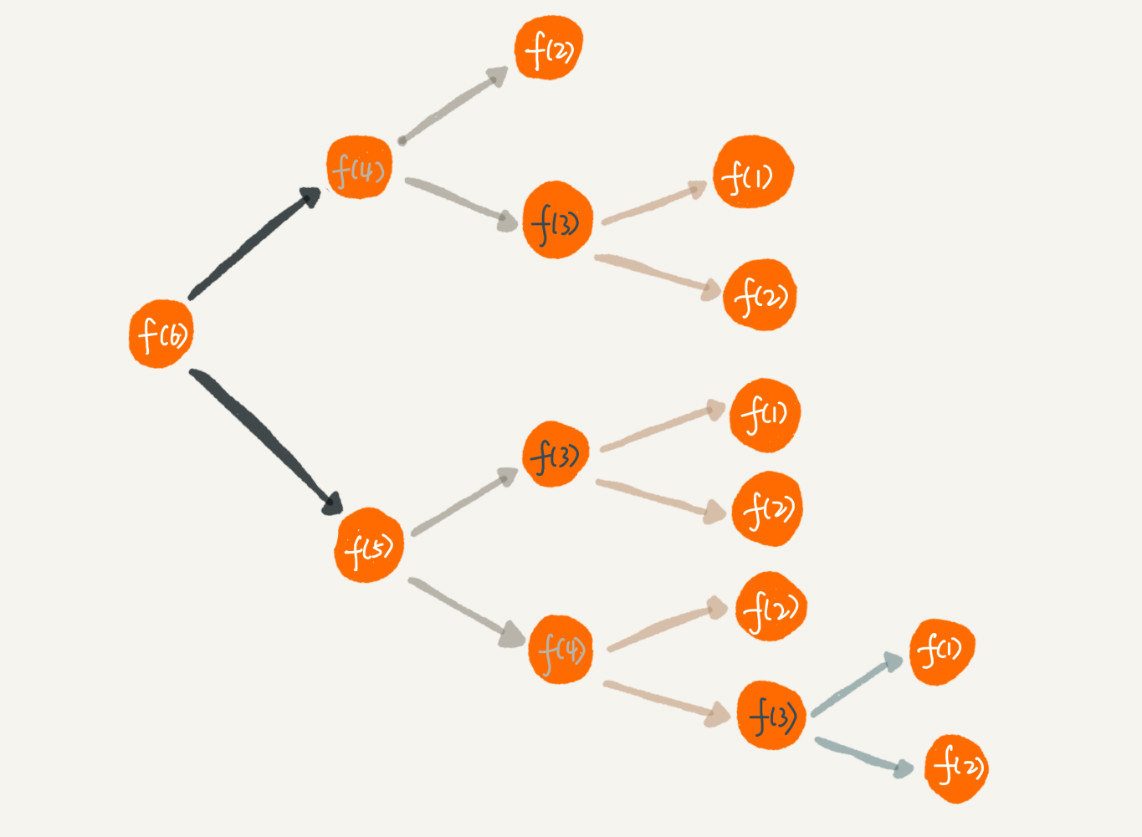
从图中,可以直观地看到:
- 计算
f(5),需要先计算f(4)和f(3) - 计算
f(4)还需要计算f(3) f(3)就被计算了很多次
这就是重复计算问题。
为了避免重复计算,可以通过一个数据结构(比如散列表)来保存已经求解过的 f(k)。当递归调用到 f(k) 时,先看下是否已经求解过了。如果是,则直接从散列表中取值返回,不需要重复计算。
将上面求解楼梯走法的代码优化:
var process = make(map[int]int) func f(n int) int { if n == 1 { return 1 } if n == 2 { return 2 } if process[n-1] != 0 { return process[n-1] + f(n-2) } process[n-1] = f(n - 1) return f(n-1) + f(n-2) } // 求解30层楼梯,从4ms下降到56us,已经不是一个数量级了
- 在时间复杂度上,递归多了很多函数调用,当这些函数调用的数量较大时,就会积聚成一个可观的时间成本
- 在空间复杂度上,递归调用一次就会在内存栈中保存一次现场数据,所以需要额外考虑这部分的开销
递归代码调试
平时调试代码使用 IDE 的单步跟踪功能,像规模比较大、递归层次很深的递归代码,几乎无法使用这种调试方式。
常用的做法:
- 打印日志发现,递归值
- 结合条件断点,golang中
Delve调试器使用delve debug进入- break设置断点
- condition设置条件
0.4. 递归改写为非递归
递归操作有点像遍历单链表,需要有指针记录前一个节点,递归代码的非递归实现,也需要有变量记录上一个步骤的结果。
递归有利有弊:
- 利:是递归代码的表达力很强,写起来非常简洁
- 弊:是空间复杂度高、有堆栈溢出的风险、存在重复计算、过多的函数调用会耗时较多等问题
所以,在开发过程中,要根据实际情况来选择是否需要用递归的方式来实现。
func f(n int) int { if n == 1 { return 1 } if n == 2 { return 2 } pre := 2 prepre := 1 ret := 0 for i := 3; i <= n; i++ { ret = pre + prepre prepre = pre pre = ret } return ret } // 求解30层楼梯,在490ns
笼统地讲,所有的递归代码都可以改为这种迭代循环的非递归写法。因为递归本身就是借助栈(系统或者虚拟机本身提供的)来实现的。
如果我们自己在内存堆上实现栈,手动模拟入栈、出栈过程,这样任何递归代码都可以改写成看上去不是递归代码的样子。但是这种思路实际上是将递归改为了“手动”递归,本质并没有变,而且也并没有解决如递归堆栈溢出或重复计算的问题,徒增了实现的复杂度。